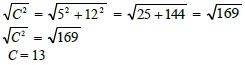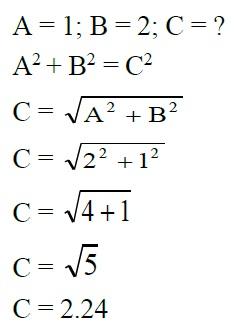Chapter 4 - Assessment Math
Assessment Rate, Mill Levies, And Tax Bill
The calculation of property tax consists of three segments: the actual value, the assessment rate, and the mill levy. The assessor establishes the actual value of the property and the classification. The Colorado Constitution states that the general assembly determines the assessment rate, and the taxing entities control the mill levies. Unfortunately, most taxpayers only understand the final result - the tax bill. It is important for assessment personnel to understand how the segments fit together in order to better explain to taxpayers the effects of changing mill levies and values.
Assessment Rate
The residential assessment rate is set by the general assembly. For a further explanation of classification, assessment rates, and level of value, refer to Chapter 6, Property Classification Guidelines and Assessment Percentages.
The classification of property influences the manner in which a property is assessed:
| Property Class | Method of Assessment |
|---|---|
| Residential | Statutory level of value at 6.25 % assessment rate for Local Governments** |
| Residential | Statutory level of value at 7.05 % assessment rate for Schools** |
| All other except producing mines, oil and gas leaseholds and lands, agricultural property, and renewable energy production property | Statutory level of value at 27 % assessment rate |
| Producing mines * | Previous calendar year’s production value, 25% of gross proceeds, or 100% of net, whichever is greater |
| Oil and gas leaseholds and lands | 87.5% of oil or gas sold or transported from premises for primary production; 75% of oil or gas sold or transported from premises for secondary and tertiary recovery |
| Agricultural Property (not including 4180/4280) | 27% of actual value, which is based on capitalizing the average net income for the 10 years preceding the level of value. The capitalization rate is set in statute, and is currently 13%. |
| Agribusiness Property - 4180/4280 | Statutory level of value at 27 % assessment rate |
| Property Class | Method of Assessment |
|---|---|
| State assessed property | Statutory level of value at 27% assessment rate |
| Exempt property | Assessed at appropriate rate but not taxed |
* There is no assessment rate applied to producing mines land. The actual and assessed values are the same figure, which is the greater of 25 percent of gross proceeds or 100 percent of net proceeds.
**For Residential properties, there are 2 assessment rates. One to be used for schools and a second to be used for all other local governments. The residential rates are assuming that the growth of the statewide actual value from 2024 to 2025 is less than or equal to 5%. If the growth is greater than 5% then the residential rates will both drop by 0.1%
Computing Assessed Value
Actual value multiplied by the appropriate assessment rate equals the assessed value of the property. For the assessment roll, the assessed value can be rounded.
Note: For the sake of simplicity, all actual and assessed values in this chapter are rounded to the nearest whole dollar.
Rounding: Rounding rules require that the number be carried one digit beyond the number to which you are rounding, discarding all numbers after that, and rounding “up” if that digit is 5 or more, and “down” if that digit is less than 5.
Example:
497.49 rounded to the nearest “tenths” is 497.5. The same number rounded to the nearest “whole number” is 497. That same number rounded to the nearest “tens” is 500.
To round to the nearest “tenths,” consider the 9 after the 0.4. This is greater than 5, causing the 0.4 to be rounded “up” to 0.5 causing the new number to be 497.5.
To round to the nearest “whole number,” discard the 9 and only consider the 0.4, 4 is less than 5, thereby the 0.49 is dropped and the number is expressed as 497.
To round to the nearest “tens” discard the 0.49 and only consider the 7, which is greater than 5, causing the 9 to be rounded “up” to 10, which carries over to 500.
- The assessed value of a commercial property is $138,003.75.
$138,003.75 rounded to the nearest $1 is $138,004 - The assessed value of a residential property is $8,406.45.
$8,406.45 rounded to the nearest $1 is $8,406 - The assessed value of production from a producing oil well is $1,330,274.75.
$1,330,274.75 rounded to the nearest $1 is $1,330,275
The assessment rate can be determined by dividing the assessed value by the actual value, assuming there is not an actual value adjustment.
Assessed value ÷ Actual value = Assessment rate
The actual value can be determined by dividing the assessed value by the assessment rate, assuming there is not an actual value adjustment.
Assessed value ÷ Assessment rate = Actual value
Mills
The English word “mill” comes from the Latin “mille,” which means one thousand. In the U.S., “mill” is a monetary term which means one one-thousandth (1/1000) of a dollar. The mill levy is the tax rate expressed in mills (thousandths of a dollar) per dollar of assessed value.
1 dime = $0.10 or 1/10 of $1.00
1 penny = $0.01 or 1/100 of $1.00
1 mill = $0.001 or 1/1000 of $1.00
The term “tax rate” is defined as the decimal equivalent of the mill levy. To convert mills to a decimal equivalent, move the decimal point three (3) places to the left. This is the equivalent of dividing the number of mills by 1,000.
75.00 mills ($75.00 per $1,000 Assessed value) = 0.075 ($0.075 per $1 Assessed value)
12.30 mills ($12.30 per $1,000 Assessed value) = 0.0123 ($0.0123 per $1 Assessed value)
Tax Rate
Tax rates are to assessed values what sales tax rates are to the cost of goods purchased. That is, the property’s assessed value is multiplied by the tax rate to determine property taxes due.
Assessed value × Tax rate = Property tax
$19,000 Assessed value × 0.047364 (47.364 mills) Tax rate = $899.92 Tax
Computing Tax Rates
Tax rates are established by the individual taxing entities and are based on the amount of money needed to provide services the following year. The budget is determined by the officials of the taxing entity. Anticipated revenues from non-property tax sources are subtracted from the total budget. The remainder is the amount required from property taxes. This amount is divided by the total assessed value in the jurisdiction to obtain the property tax rate.
Section 20, art. X, COLO. CONST., and Colorado Revised Statutes place limitations on mill levy and spending and revenue increases for taxing entities. For further explanation, refer to Chapter 7, Abstract, Certification, and Tax Warrant.
The total tax rate applied to an individual property is determined by adding together the separate rates of all taxing entities having jurisdiction in the specific area where the property is located.
Example:
Mr. Smith’s store is located within the boundaries of:
The county
An incorporated city
A school district
A water and sanitation district
Each taxing entity has set its budget and determined the tax rate necessary to obtain the required revenue from property taxation. Determine the total tax rate applicable to Mr. Smith’s store by adding together the rates of the four taxing districts:
| County | 0.021925 |
|---|---|
| City | 0.011654 |
| School district | 0.059467 |
| Water and sanitation district | 0.002919 |
| Total tax rate | 0.095965 (95.965 Mills) |
The total tax rate of 0.095965 can be expressed three different ways:
95.965 mills or
$95.965 per $1,000 of assessed value or
9.5965% of the assessed value
To convert mills to a percentage, move the decimal point one place to the left. Remember, the tax rate is the decimal equivalent of the mill levy.
Computing Individual Tax Bills
Multiply the total assessed valuation of the property by the total tax rate for the tax area:
Example:
Mr. Smith’s store building and land are appraised at $100,000 actual value. The property’s assessed value, at 27 % of actual value, is $27,000. The tax rates for the area are: 0.059467 for the school district, 0.021925 for the county, 0.011654 for the city, and 0.002919 for the water and sanitation district; for a total tax rate of 0.095965. What is Mr. Smith’s tax?
Once the total tax rate is determined, it is a simple matter to calculate the individual tax bill.
$ 100,000 Actual value
× 0.27 Assessment rate
= $ 27,000 Assessed value
× 0.095965 Tax rate
= $2,591.06 Tax
Whether the tax rate is expressed in mills, $ per $1,000 assessed value, or a percentage of assessed value, the taxes calculated will always be the same.
Using a Mill Levy and Assessed Value
95.965 Mill levy:
Convert the mill levy to a decimal equivalent tax rate by moving the decimal point three places to the left and multiply by the assessed value.
95.965 Mill levy = 0.095965 Tax rate
0.095965 Tax rate × $27,000 Assessed value = $2,591.06 Tax
Using $ Per $1,000 in Assessed Value
$95.965 per $1,000 of assessed valuation:
Divide the assessed value by 1,000 and multiply by tax $ per $1,000 assessed value.
$27,000 Assessed value ÷ $1,000 = 27.00
27.00 × $95.965 (per $1,000 Assessed value) = $2591.06 Tax
Using Percentage of Assessed Value
9.5965% of assessed value:
Convert the percent (%) of assessed value to a decimal equivalent by moving the decimal point two places to the left and then multiplying by the assessed value.
9.5965% = 0.095965 Tax rate
0.095965 Tax rate × $27,000 Assessed value = $2,591.06 Tax
Example:
Using the following individual tax rates, calculate the taxes for a residence with an actual value of $100,000.
County ....................................21.925..........= 0.021925
City .........................................11.654..........= 0.011654
School district ........................59.467..........= 0.059467
Water and sanitation district .. 2.919..........= 0.002919
Total tax rate 95.965 Mills = 0.095965
Residential value:
School: $100,000 Actual value × .0705 Assessment rate = $7,050 Assessed value
School: $7,050 Assessed value × 0.059467 Tax rate = $419.24 Tax for School
Local Government: $100,000 Actual value × .0625 Assessment rate = $6,250 Assessed value
Local Government: $6,250 Assessed value × 0.036498 Tax rate = $228.11 Tax for Local Government
Total Tax: $419.24 + $228.11 = $647.35 Tax
Computing Documentary Fees
A documentary fee is a fee imposed by the clerk and recorder for any deed or instrument presented for recordation in which the consideration for the real property is over $500. Exclusions from the documentary fee exist and can be found in § 39-13-104, C.R.S. The documentary fee is computed at the rate of one cent for each one hundred dollars of consideration ($0.01 per $100), § 39-13-102, C.R.S.
Example:
A warranty deed has been recorded with a consideration of $350,000, the county clerk and recorder will need to collect a documentary fee based on the consideration. Calculate the documentary fee based on the consideration provided.
Warranty deed consideration: = $350,000 ÷ $ 100 = $ 3,500 × $ 0.01 = Documentary fee $ 35.00
A warranty deed has been recorded with a documentary fee of $35.00, what is the consideration listed on the deed?
Documentary fee = $ 35.00 ÷ $ 0.01 = $ 3,500 × $ 100 Warranty deed consideration: $350,000
Refer to ARL Volume 3, Real Property Valuation Manual, Chapter 3, Sales Confirmation and Stratification, for additional information regarding documentary fees.
Computing Real Property Transfer Declaration Penalty
Whenever a conveyance document is presented for recordation, a copy of a Real Property Transfer Declaration (TD-1000) should be included. If the declaration is not returned within 30 days, the assessor may impose a penalty equal to $25 or 0.025% (0.00025) of the property’s sales price, whichever is greater, §§ 39-14-102 and 39-14-103, C.R.S.
Example:
A warranty deed has been recorded with a consideration of $165,000, the county clerk and recorder has collected a documentary fee of $16.50; however, a transfer declaration was not submitted. Determine the penalty that should be collected by the county assessor if no declaration is submitted by the grantee.
Documentary fee $16.50
Property sales price $165,000
$165,000 × 0.00025 = $41.25, penalty
Fractional Interests, Decimals, and Percentages
Definitions
Fraction: One or more parts of a whole. (1/4 is a part of the whole 4/4)
Numerator: The top number of a fraction.
Denominator: The bottom number of a fraction.
Common denominator: A number in which all the denominators of a set of fractions may be divided into evenly.
Decimal equivalents: A fraction converted to a decimal. 1/4 = 0.25, 4/4 = 1.00
Converting to Lowest Common Denominator
To properly allocate fractional interests, each fraction should be expressed using the lowest common denominator. The first step in determining the lowest common denominator is to reduce fractions to their lowest fractional form.
60/360 reduces evenly to 1/6. (Divide the denominator by the numerator. If the result is a whole number, that number is the new denominator.)
Then, determine the lowest common denominator. The lowest common denominator can be defined as the lowest number that can be divided evenly by all denominators without leaving a remainder. Multiply the numerator by the same number needed to convert the denominator to the lowest common denominator.
Example:
The following interests total the whole interest in a property. Convert the fractions to lowest common denominators. Determine a number that is evenly divisible by 2, 5, and 10. Answer: 10 (2 × 5 = 10). Ten becomes the lowest common denominator because each fraction will convert to “tenths.”
Convert all fractions to the same common denominator or “tenths.” Multiply the numerator of each fraction by the number used to convert its denominator to the lowest common denominator.
1/10 does not need to be converted because it is already in “tenths.”
2/5 × 2/2 = 4/10
1/2 × 5/5 = 5/10
Summary of Conversions:
| Interest | Common Denominator | Conversion | Converted Fraction |
|---|---|---|---|
| 1/10 | 10 | (10 ÷ 10 = 1; 1 × 1 = 1) | 1/10 |
| 2/5 | 10 | (10 ÷ 5 = 2; 2 × 2 = 4) | 4/10 |
| 1/2 | 10 | (10 ÷ 2 = 5; 5 × 1 = 5) | 5/10 |
| 10/10 |
In this example, the ownership interests, when added together, should equal “one.” Add the new fractions to be sure they total “the whole.”
1/10 + 4/10 + 5/10 = 10/10
This method is typically used when calculating undivided interests. Property is often transferred to several individuals, each having a different undivided interest.
Example: Determine the fractional amount of mineral interest severed from the surface ownership and the amount of mineral interest remaining with the surface ownership.
There is an existing 3/8 severed mineral interest reservation in the S1/2 S32 T13 R44. Your office receives two deeds on the same legal description. One contains a mineral reservation of 60/360 and the second deed contains a mineral reservation of 50/120.
| Interest | Lowest Fractional Form | Fractional Form using Common Denominator |
|---|---|---|
| 3/8 | 3/8 | 9/24 |
| 60/360 | 1/6 | 4/24 |
| 50/120 | 5/12 | 10/24 |
| 24/24 |
23/24 represents the total severed mineral interest (24/24 - 23/24 = 1/24)
1/24 is the mineral interest remaining with the surface estate.
Fraction of a Fraction
It is sometimes necessary to determine the acreage or value amount for a partial interest of a fractional interest.
Example:
1/8 of 3/4 interest
To calculate, multiply the fractions: 1/8 × 3/4 = 3/32
Example:
A personal representative’s deed stipulates that Mrs. White’s children are to receive her 1/4 interest in 148 mineral acres. Her son receives a 1/3 undivided interest, one daughter receives a 1/4 undivided interest, and a second daughter receives a 5/12 undivided interest in the 1/4 interest.
Using fractions, determine the number of mineral acres assigned to each undivided interest and the actual value for each interest. The actual value for severed minerals is $7 per mineral acre.
Below are three options for calculating the mineral acreage for each undivided interest.
Option 1:
First, determine a fractional representation of each person’s inherited interest in Mrs. White’s interest.
| Children's Interests | Mrs. White's Interests |
|---|---|
| 1/3 x | 1/4 = 1/12 |
| 1/4 x | 1/4 = 1/16 |
| 5/12 x | 1/4 = 5/48 |
Second, determine the acreage amount for each interest. Mrs. White owned 1/4 interest in 148 mineral acres.
1/12 × 148 Mineral acres = 148 ÷ 12 × 1 = 12.33 Mineral acres
1/16 × 148 Mineral acres = 148 ÷ 16 × 1 = 9.25 Mineral acres
5/48 × 148 Mineral acres = 148 ÷ 48 × 5 = 15.42 Mineral acres
37.00 Mineral acres
Option 2:
Using the mineral acreage owned by Mrs. White, determine the acreage amount for each person’s interest.
1/4 of 148 Mineral acres = 37 Mineral acres (full 1/4 interest)
1/3 × 37/1 = 12.33 Mineral acres
1/4 × 37/1 = 9.25 Mineral acres
5/12 × 37/1 = 15.42 Mineral acres
37.00 Mineral acres
Option 3: You may combine the two steps above as follows:
| Children's Interests | Mrs. White's Interests |
|---|---|
| 1/3 x | 1/4 x 148 = 12.33 Mineral acres |
| 1/4 x | 1/4 x 148 = 9.25 Mineral acres |
| 5/12 x | 1/4 x 148 = 15.42 Mineral acres |
| 37 Mineral acres |
Calculate the actual value of each interest.
| Children's Interests | Mrs. White's Interests | Actual Value |
|---|---|---|
| 1/3 | 12.33 Mineral acres x $7 per acre | = $86 Actual value |
| 1/4 | 9.25 Mineral acres x $7 per acre | = $65 Actual value |
| 5/12 | 15.42 Mineral acres x $7 per acre | = $108 Actual value |
Changing a Fraction to its Decimal Equivalent
Divide the numerator (top number) by the denominator (bottom number).
Example:
Which of these fractions is the greatest? 1/3, 1/4, 5/12, or 9/32
1 ÷ 3 = 0.33333
1 ÷ 4 = 0.25000
5 ÷ 12 = 0.41667
9 ÷ 32 = 0.28125
5/12 is the greatest amount.
Example:
By personal representative’s deed, Mrs. Brown’s severed mineral interest in 640 acres is conveyed to her four children. Her son received a 9/15 undivided interest, and each of her 3 daughters received a 2/15 undivided interest. The current actual value of the severed mineral interest is $4,480. Determine the actual value attributable to each undivided interest. The actual value for severed minerals is $7 per mineral acre.
Decimal equivalent of son’s 9/15 interest: 9 ÷ 15 = 0.60
Decimal equivalent of each daughter’s 2/15 interest: 2 ÷ 15 = 0.1333
Value calculation:
Son:
640 Mineral acres × 0.60 Son’s interest = 384 Mineral acres
384 Mineral acres × $7 Per acre = $2,688 Son’s actual value
Daughters:
640 Mineral acres × 0.1333 Daughter’s interest = 85.312 Mineral acres
85.312 Mineral acres × $7 Per acre = $597 Daughter’s actual value
Son $2,688 Actual value
Daughter 1 597 Actual value
Daughter 2 597 Actual value
Daughter 3 597 Actual value
$4,479 Total Actual value
Due to rounding, the sum of the individual interests is $1 less than the total actual value. Therefore, the actual value of the son’s interest is increased by $1 to ensure that the total actual value remains the same.
Son $2,689 Actual value
Daughter 1 597 Actual value
Daughter 2 597 Actual value
Daughter 3 597 Actual value
$4,480 Total actual value
Note: The value of the largest undivided interest holder receives the rounding adjustment.
Example:
Paul Jones purchased a severed mineral interest. The mineral deed described the interest as a 768/4096 severed mineral interest in a certain half section of land containing 320 acres. The actual value for severed minerals is $7 per acre. Determine the actual value of Mr. Jones’ mineral interest.
The decimal equivalent of Jones’ 768/4096 mineral interest is:
768 ÷ 4096 = 0.1875
The actual value of Mr. Jones’ severed mineral interest is:
320 Acres × 0.1875 Jones’s interest = 60 Mineral acres
60 Mineral acres × $7 Per acre = $420 Actual value
Converting Decimal Equivalents to Percentages
To convert a decimal to a percentage, move the decimal point two places to the right and add the “%” sign.
Example:
0.125 = 12.5%
0.0197 = 1.97%
Converting Percentages to Decimal Equivalents
“Percent” means “per one hundred.” The term 15% means 15 parts per hundred or 15/100. It can also be written as 0.15, which is the result of dividing 15 by 100.
To convert a percentage to its decimal equivalent, drop the percent symbol (%) or the word “percent,” and move the decimal point 2 places to the left.
Example:
12.5% = 0.125
1.97% = 0.0197
Interest in Joint Tenancy
Upon the death of a joint tenant, and there is one surviving joint tenant, the interest automatically vests with the surviving joint tenant. In the case of two or more surviving joint tenants, the decedent’s interest vests proportional to their respective interests at the time the joint tenancy was created, § 38-31-101(6)(c), C.R.S.
Example:
Mary, Bill, and Jack own a parcel in joint tenancy, with Mary owning 1/2 interest, Bill owning 1/4 interest and Jack owning 1/4 interest. Jack dies; therefore, his 1/4 interest must be divided between Mary and Bill proportional to their respective interests at the time the joint tenancy was created.
Below are three options for calculating each person’s interest.
Option 1:
The three individuals own 4/4 total interest; Mary has 2/4 interest or 2 parts and Bill and Jack each have 1/4 interest or 1 part each. Mary and Bill retain their interests, which equals three parts; therefore, the 1/4 interest owned by Jack must be divided into 3 parts.
1/4 = 1/4 × 3/3 = 3/12. Each part equals 1/12 with Mary receiving 2 parts or 2/12 and Bill receiving 1 part or 1/12.
Mary: 6/12 (1/2) + 2/12 = 8/12 or 2/3
Bill: 3/12 (1/4) + 1/12 = 4/12 or 1/3
3/3 or 1
Mary now owns 2/3 interest and Bill owns 1/3 interest.
Option 2:
To calculate the remaining interests, divide the other interests by one minus the deceased interest or (1-1/4) as follows:
1 - 1/4 = 3/4 (to divide by a fraction, invert it and multiply)
Bill: 1/4 divided by 3/4 = 1/4 × 4/3 = 4/12 = 1/3
Mary: 1/2 divided by 3/4 = 1/2 × 4/3 = 4/6 = 2/3
3/3 or 1
Option 3:
Convert the fractional interests to a percentage.
Mary owns 50% interest, Bill owns 25% interest and Jack owns 25% interest. If Jack dies, his percent of interest is subtracted from the full 100% (100% - 25% = 75%). To calculate the proportional share of the ownership interests, the original percent of the interest held serves as the numerator and 0.75 is used as the denominator.
0.50 ÷ 0.75 = 66.7% Mary
0.25 ÷ 0.75 = 33.3% Bill
100.0%
Computing Areas
Computing the area of a shape requires the use of mathematical formulas. Many formulas are quite complex; however, most of the work accomplished by the assessor’s office can be handled easily with plane shape geometry concepts. Plane shape geometry is the study of figures in two dimensions having only width and length. Some of the common geometric terms are defined below.
Definitions
Area: The measure of a surface, generally expressed in square units, such as, square feet, square miles, acres.
Circle: A closed curve such that any point on the curve is equidistant from a fixed point called the center.
Circumference: The distance around the outside of a circle.
Diameter: Two times the radius of a circle (2r). It can also be defined as, the length of a straight line from one side of a circle to the other side, passing through the center of the circle.
Parallelogram: A four-sided polygon with opposite sides equal and parallel.
Perimeter: The total distance around the figure, expressed in linear units, such as feet, miles, yards.
Pi: Typically shown as the Greek letter “π” it is the ratio of any circle’s circumference to its diameter. π = Circumference ÷ Diameter; π is a constant 3.1416.
Plane: A flat surface defined by any three points not in a straight line.
Polygon: A closed figure whose sides are straight lines. Common polygons include squares, rectangles, trapezoids, triangles, and parallelograms.
Radius: The distance from the center of a circle to any point on the circumference (r).
Rectangle: A four-sided polygon with opposite sides equal and parallel and four right angles.
Right angle: An angle equaling 90°.
Square: A four-sided polygon with equal sides and four right angles.
Trapezoid: A four-sided polygon having only two parallel sides.
Triangle: A three-sided polygon.
Formulas
The mathematical formulas required to calculate areas, perimeters, and circumference are listed below.
Area:
Square: Base × Height (or Base2)
Rectangle: Base × Height
Parallelogram: Base × Height
(The height is measured at a right angle (90º) to parallel sides.)
Trapezoid: (Parallel side 1 + Parallel side 2) divided by 2 × Height
(The height is measured at a right angle (90º) to parallel sides.)
Triangle: Base × Height ÷ 2
Circle: π r2
Perimeters: The sum of the sides.
Circumference: 2πr or πd where r is the radius and d is the diameter of the circle.
Example – Areas and perimeters of polygons.
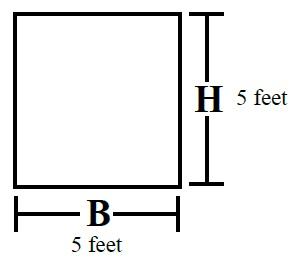
Square
Formula
B × H = Area
5 Feet × 5 Feet = 25 Square feet
Perimeter = 5 + 5 + 5 + 5 = 20 Feet
Characteristics
- Opposite sides are parallel.
- All sides are equal.
- All angles = 90° (right).
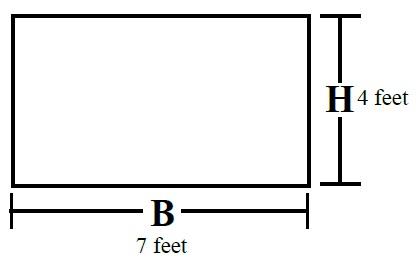
Rectangle
Formula
B × H = Area
7 Feet × 4 Feet =28 Square feet
Perimeter = 7 + 4 + 7 + 4 = 22 Feet
Characteristics
- Opposite sides are parallel.
- Opposite sides are equal.
- All angles = 90° (right).
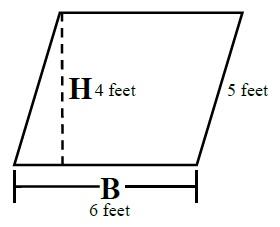
Parallelogram
Formula
B × H* = Area
6 Feet × 4 Feet = 24 Square feet
Perimeter = 5 + 6 + 5 + 6 = 22 Feet
Characteristics
- Opposite sides are parallel.
- Opposite sides are equal.
- Angles may not be 90°.
- *Height is measured at right angle (90°) to parallel sides
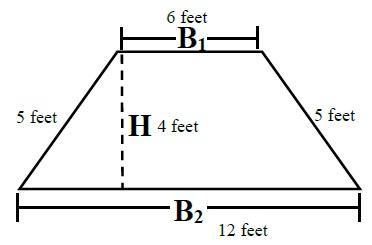
Trapezoid
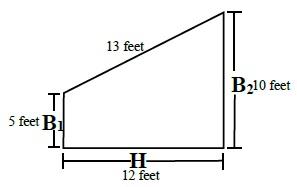
To calculate the area of a trapezoid, you must first determine the parallel sides; these are the bases. The height is then measured as the perpendicular distance between the two parallel sides.
Formula
(B1 + B2) ÷ 2 × H* = Area
(6 Feet + 12 Feet) ÷ 2 = 9 Feet
9 Feet × 4 Feet = 36 Square feet
Perimeter = 6 + 5 + 12 + 5 = 28 Feet
Characteristics
- Two measured sides are parallel.
- *Height is measured at right angle (90°) to parallel sides.
Formula
(B1 + B2) ÷ 2 × H* = Area
(5 Feet + 10 Feet) 2 = 7.5 Feet
7.5 Feet × 12 Feet = 90 Square feet
Perimeter = 5 + 13 + 10 + 12 = 40 Feet
Characteristics
- Two measured sides are parallel.
- *Height is measured at right angle (90°) to parallel sides.
Triangles
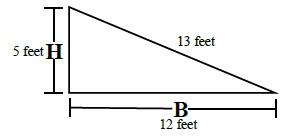
Right Triangle
Formula
Area = (B × H*) ÷ 2
(5 Feet × 12 Feet) 2 = 30 Square feet
Characteristics
- One angle equals 90°.
- *Height is measure of the side that forms a right angle (90°) with the base.
If the length of one side of a right triangle is missing, you can determine its length by using the following equation:
A2 + B2 = C2, where A and B are the lengths of the sides forming the 90° angle, and C = the hypotenuse (the longest side).
Using the example above, if A = 5 Feet and B = 12 Feet, then the formula A2 + B2 = C2 becomes 52 + 122 = C2 and C2 = 25 + 144 = 169 Square feet. To determine C, take the square root of both side of the equation as follows:
Therefore, the perimeter of the above triangle will be 5 Feet + 12 Feet + 13 Feet = 30 Feet
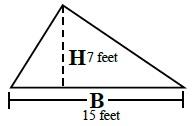
Acute Triangle
Formula
Area = (B × H*) ÷ 2
(5 Feet × 12 Feet) ÷ 2 = 30 Square feet
Characteristics
- All angles less than 90° for a total of 180°.
- *Height measured at a right angle (90°) from the base to the highest point of the triangle.
The perimeter can only be determined if you know where the height intersects the base.
This will give you two sides of the triangle so you are able to determine the third side.
See A2 + B2 = C2 formula above in right triangle example.
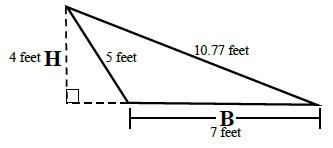
Obtuse Triangle – calculating the area when the base and height are known
Formula
(B × H*) ÷ 2 = Area
(7 Feet × 4 Feet) 2 = 14 Square feet
Perimeter = 5 + 7 + 10.77 = 22.77 Feet
Characteristics
- One angle measures more than 90°.
- *Height measured at a right angles angles (90°) from the base (extended outside of the triangle) to the highest point of the triangle.
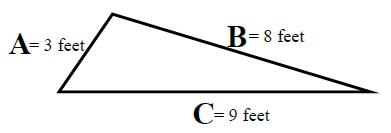
Obtuse Triangle – calculating the area when the three sides are known
The area of a triangle can be found, without knowing the height, by using the following formula.
Formula
S = (A + B + C) ÷ 2
S = (3 Ft + 8 Ft + 9 Ft) ÷ 2 = 10 Feet
Characteristics
- One angle measures more than 90°.
- Height is not known, but three sides are known; thus, the given equations are used to find the area.
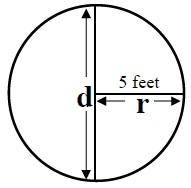
Circles
Formula
πr2 = Area
π × (5 Feet)2 = (π × 25) = 78.54 Square feet
Circumference = 2πr = 31.42 Feet
Characteristics
- π is the ratio of any circle's circumference to its diameter.
- π = 3.1416
- r-radius; d=diameter 2r=diameter
As indicated previously, “r” is the radius. To calculate the circumference, the formula is 2πr or, since 2 times the radius equals the diameter (d), the formula becomes πd. For the area, the formula is π times the square of the radius. Any number squared is
that number multiplied by itself. In the figure above, the radius is five feet, thus the radius squared is 5 times 5, or 25.
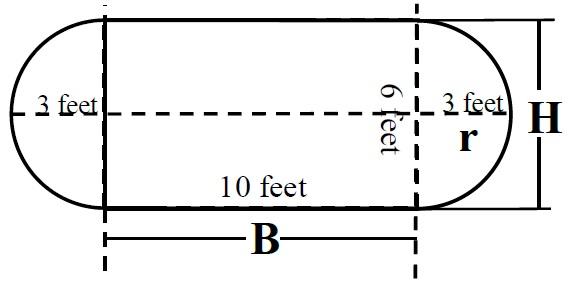
Find the Area and Perimeter of the Diagram Shown Below:
Formula
(πr2) + (B × H) = Area
Characteristics
- Figure is composed of a rectangle and two half-circles
To calculate the area:
First, find the area of the two half-circles:
The area of one half-circle is: (πr2) ÷ 2
This is equal to (3.1416 × 32) ÷ 2 = 14.137 Square feet.
Since the two half-circles are equal, the result can be multiplied by 2. Therefore, the area of the two half-circles is 28.274 square feet, which is also the area of one whole circle.
Second, find the area of the rectangle: 10 × 6, which equals 60 square feet.
Third, calculate the total area of the figure, by adding the two areas together:
28.27 Square feet + 60 Square feet = 88.27 Square feet.
To calculate the perimeter:
Perimeter = (2πr) + (2 × B)
First, find the perimeter of the half-circles. Since each half-circle is the same, we need only find the perimeter of the whole circle. This distance is 2πr or πd, which equals 6 × 3.1416, which equals 18.85 feet.
The remaining sides for calculation of the perimeter are 10 + 10, which equals 20 feet.
Add the two amounts together for the total perimeter:
18.85 Feet + 20 Feet = 38.85 Feet
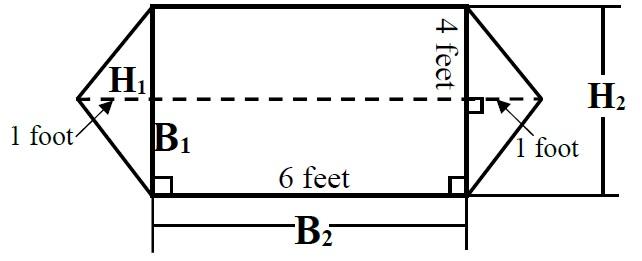
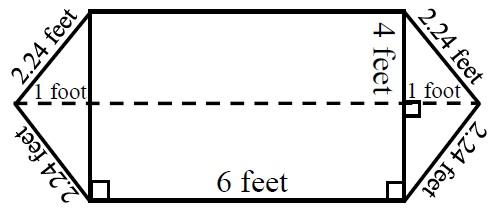
Find the Area and Perimeter of the Diagram Shown Below:
To calculate the area:
First, find the area of the two triangles at the ends of the figure:
The information given indicates that the two triangles are identical; therefore, we need only find the area of one triangle and multiply the result by 2. The formula for a triangle is base multiplied by the height divided by 2. This is equal to (1 × 4) ÷ 2 = 2 square feet.
The area of the two triangles is 4 square feet.
Second, calculate the area of the rectangle: 6 × 4, which equals 24 square feet.
Third, calculate the total area of the figure, by adding the two areas together:
4 Square feet + 24 Square feet = 28 Square feet
The perimeter can be determined by using the right triangle formula, namely, A2 + B2 = C2 where C = the hypotenuse (the longest side) of a right triangle and A and B are the sides.
The hypotenuse is the side we are interested in for the determination of the perimeter. To find the hypotenuse, take the square root of the sum of the squares of the sides.
To calculate the perimeter:
Perimeter = 2.24 + 2.24 + 6 + 2.24 + 2.24 + 6 = 20.96 Feet
Converting Units of Measure
Areas are expressed in square units of measure, such as square feet, square inches, or square miles. Sometimes it is necessary to convert one unit of measure to another unit of measure. For instance, to convert square feet to acres, divide the number of square feet by 43,560, which is the number of square feet in one acre.
Example: Convert 1,000,000 square feet to acres.
1,000,000 Square feet ÷ 43,560 = 22.96 Acres
Example: Convert 1,000,000 square feet to square yards.
A yard is 3 feet in length; therefore, one square yard equals 3 feet × 3 feet or 9 square feet.
1,000,000 Square feet ÷ 9 Square feet = 111,111.11 Square yards
Basic Assessment Statistics
The following is information on selected statistical measures, based on accumulated sales ratios. These measures can be valuable tools in analyzing such ratios. Additional detail and explanation can be found in ARL Volume 3, Real Property Valuation Manual, Chapter 8, Statistical Measurements.
Sales Ratio Studies
A sales ratio is the relationship of the assessor’s actual value to the selling price, usually expressed as a percentage.
Computation
The sales ratio is computed by dividing the assessor’s actual value of the sold property by its sales price.
Example:
| Parcel | Actual Value | ÷ Sales Price | = Ratio |
|---|---|---|---|
| 1 | $169,000 | $157,500 | 1.0730 |
| 2 | $115,000 | $108,000 | 1.0648 |
| 3 | $ 89,900 | $ 93,900 | 0.9574 |
| 4 | $ 46,500 | $ 51,800 | 0.8977 |
| 5 | $ 64,200 | $ 77,300 | 0.8305 |
Essential Aspects
Sales ratio studies are used to evaluate the fairness and uniformity of the distribution of the tax burden. The two essential aspects of a sales ratio study are assessment level and assessment uniformity. Assessment level is indicated by computing the central tendency of the ratios and is called the median sales ratio. Assessment uniformity is indicated by comparing the measures of central tendency of different types of property groups. The most common measure of assessment uniformity is the coefficient of dispersion (COD).
Measures of Central Tendency
A measure of central tendency is a single number or value that expresses the center or the middle of a set of data. The central tendency may be considered representative or typical of the entire data set. The three measures of central tendency used in assessment ratio studies are the mean, median, and weighted mean.
Median
The median is the value that divides the data in half, each half containing the same number of observations. There are as many values above the median as below it. In assessment ratio studies, the median is generally used in measuring the assessment level because the median is least affected by “outlier” data. Outliers are properties with very high or very low sales ratios.
To determine the median, a data array must be constructed. An array lists the data from lowest to highest or highest to lowest. The rank of the median can be determined by the formula:
N = Number of observations
(N + 1) ÷ 2
Example: Find the median ratio of the data set. Ratios are arrayed, not the actual values or sales prices.
| Parcel | Actual Value | Sales Price | Ratio Arrayed |
|---|---|---|---|
| 1 | $169,000 | $157,500 | 1.0730 |
| 2 | $115,000 | $108,000 | 1.0648 |
| 3 | $ 89,900 | $ 93,900 | 0.9574 Median |
| 4 | $ 46,500 | $ 51,800 | 0.8977 |
| 5 | $ 64,200 | $ 77,300 | 0.8305 |
(5 + 1) ÷ 2 = 3
The median is the middle value in the array from either the top or the bottom of the array.
If there is an even number of values, the median is the average of the two middle values.
Advantages:
- Easy to determine.
- Unaffected by extremely high or low values, so it is a stable measure of central tendency.
- The median always exists for any set of data.
- There can be only one median.
- The median takes all data into account.
Disadvantages:
- The data must first be arrayed.
- The median must be calculated if there is an even number of values in the data set.
Mean
The mean is the average of the data. The mean is computed by dividing the sum of the values in the data set by the number of observations.
Example: Find the mean ratio of the data set.
| Parcel | Actual Value | Sales Price | Ratio Arrayed |
|---|---|---|---|
| 1 | $169,000 | $157,500 | 1.0730 |
| 2 | $115,000 | $108,000 | 1.0648 |
| 3 | $ 89,900 | $ 93,900 | 0.9574 |
| 4 | $ 46,500 | $ 51,800 | 0.8977 |
| 5 | $ 64,200 | $ 77,300 | 0.8305 |
| Total | 4.8234 |
Sum of ratios ÷ Number of ratios = Mean ratio
4.8234 Sum of ratios ÷ 5 Number of ratios = 0.9647 Mean ratio
Advantages:
- Not difficult to compute.
- Mean can be computed for any set of data.
- The mean takes all the data into account.
Disadvantages:
- The mean is greatly affected by extremely high and low values (outliers).
Weighted Mean
The weighted mean ratio is the ratio of the total actual values to the total sales prices in a group. The weighted mean measures assessment level on a dollar-by-dollar basis whereas the mean and median do so on a property-by-property basis.
Example: Find the weighted mean of the data set.
| Parcel | Actual Value | Sales Price |
|---|---|---|
| 1 | $169,000 | $157,500 |
| 2 | $115,000 | $108,000 |
| 3 | $ 89,900 | $ 93,900 |
| 4 | $ 46,500 | $ 51,800 |
| 5 | $ 64,200 | $ 77,300 |
| Total | $484,600 | $488,500 |
Sum of actual values ÷ Sum of sales prices = Weighted mean
$484,600 Sum of actual values ÷ $488,500 Sum of sales prices = 0.9920 Weighted mean
Measures of Dispersion (Variation or Spread)
Measures of central tendency indicate only the general or overall level to which properties are appraised. They do not indicate the amount of variation or spread within the data set. In order to gain a more accurate picture of the equity and uniformity within the data set, measures of dispersion or variability are also needed. Consider the following two groups of ratios:
Neighborhood A
0.96
0.95
1.00
1.02
1.04
5.00 Total
Median = 1.00
Mean = 1.00
Neighborhood B
0.50
0.80
1.00
1.20
1.50
5.00 Total
Median = 1.00
Mean = 1.00
Both neighborhoods have the same median and mean sales ratio. It is obvious, however, that the properties in neighborhood A are appraised more equitably and uniformly than those in neighborhood B. Thus, the need for a measurement of variability.
Other Examples of Dispersion or Variability:
Moderate dispersion:
Considerable dispersion:
No dispersion:
Measures of dispersion or variability are either absolute or relative.
Absolute Measures
- Range
- Variance
- Standard Deviation
- Average Mean Absolute Deviation
- Average Median Absolute Deviation
Relative Measures
- Coefficient of Dispersion
- Coefficient of Variation
Absolute Measure
Median deviation is the average of the absolute deviations of the observations from their own median value. The absolute deviation is calculated by subtracting the median from the sales ratio. The resulting number will be treated as “absolute” or without a positive or negative sign.
Absolute value is defined as the value of a number regardless of its sign, e.g., the numbers (3) and (-3) both have an absolute value of 3.
Example:
| Parcel | Sales Ratio | - Median | = Absolute Deviation from Median |
|---|---|---|---|
| 1 | 1.0730 | 0.9574 | 0.1156 |
| 2 | 1.0648 | 0.9574 | 0.1074 |
| 3 | 0.9574 Median | 0.9574 | 0.0000 |
| 4 | 0.8977 | 0.9574 | 0.0597 |
| 5 | 0.8305 | 0.9574 | 0.1269 |
| 0.4096 |
Sum of absolute deviations from median / Number of observations = Average absolute deviation from the median
0.4096 ÷ 5 = 0.0819
Advantages and disadvantages:
The average absolute deviation from the median requires somewhat involved computation, but it uses all the data items, and it is a good measure of the typical dispersion among the items. It is not severely affected by an occasional very high or very low value among the observations.
Relative Measure
The coefficient of dispersion (COD) is a relative measure of dispersion. It measures the amount of dispersion among the observations in a set of data compared to a measure of central tendency for the same data set. The COD is a measure of dispersion widely used in assessment work. It is computed as follows:
(Average absolute deviation from the median ÷ Median sales ratio) × 100 = COD
It is the percentage by which the various individual sales ratios differ, on the average, from the median or mean ratio. The COD is the single most useful measure of assessment variability. Six steps are required to calculate the COD:
- Compute the difference between each sales ratio and the measure of central tendency. The measure of central tendency used by the assessor’s office is the median.
- Take the absolute value of the difference.
- Sum the absolute differences.
- Divide that sum by the number of observations (N) to obtain the average deviation.
- Divide the average deviation by the appropriate measure of central tendency (the median).
- Multiply that quotient by 100.
For assessment work, the usual method is the absolute deviation from the median divided by the median sales ratio. This is because the absolute deviation from the median is a stable measure of dispersion, and the median sales ratio is a stable measure of central tendency, especially when there are extreme data values.
Example:
| Parcel | Sales Ratio | - Median | = Absolute Deviation from Median |
|---|---|---|---|
| 1 | 1.0730 | 0.9574 | 0.1156 |
| 2 | 1.0648 | 0.9574 | 0.1074 |
| 3 | 0.9574 | 0.9574 | 0.0000 |
| 4 | 0.8977 | 0.9574 | 0.0597 |
| 5 | 0.8305 | 0.9574 | 0.1269 |
| 0.4096 |
0.4096 ÷ 5 = 0.0819 Average Absolute Deviation from the Median
Coefficient of Dispersion:
(Average absolute deviation from the median ÷ Median sales ratio) × 100 = COD
(0.0819 ÷ 0.9574) × 100 = 8.554 COD
Prorating Values
All property, real and personal, located in the state at 12:00 noon on January 1 is considered taxable unless expressly exempted by the Constitution or state statutes, § 39-1-105, C.R.S.
Statute requires all property in the state to be valued based on the condition and location of the property on January 1 of the assessment year. Certain exceptions to the rule require the assessor’s office to prorate values according to the period of time the property was legally taxable. The word “prorate” means to divide or distribute proportionately. Circumstances where proration/apportionment is required by law are:
- Real property that was destroyed after the assessment date, § 39-5-117, C.R.S.
- Real property that becomes exempt after the assessment date, §§ 39-3-124, 39-3-129, and 130(1)(a)(I), C.R.S.
- Exempt real property that becomes taxable after the assessment date, §§ 39-3-124, 39-3-129, and 130(1)(b)(I), C.R.S.
- Titled manufactured homes that enter or leave the state after the assessment date, §§ 39-5-204(1)(c)(II), and 205(3)(b), C.R.S.
- Manufactured homes located on sales display lots of manufactured home dealers and listed as inventories of merchandise by the dealer are exempt, § 39-5-203(3)(a), C.R.S. If the manufactured home becomes part of the dealer’s inventory and located on a display lot or is removed from the display lot to a taxable location, the value is prorated by the day, based on the date the home changed taxable status.
- The value of movable equipment and oil and gas rotary drilling rigs that enter or leave the county after the assessment date is apportioned between affected counties according to amount of time spent in each county, §§ 39-5-113 and 113.3, C.R.S.
- Works of art qualify for a property tax exemption when the works of art are in the custody and control of the state or a political subdivision thereof, a library or any art gallery or museum which is owned or operated by a charitable organization whose property is irrevocably dedicated to charitable purposes and whose assets shall not inure to the benefit of any private person. The exemption applies only for the period of time the works of art are actually on loan, §§ 39-1-102(18), 39-3-123, and 39-5-113.5, C.R.S.
General Proration Rules
Prorate the actual value to the exact number of days the real property was legally taxable, except when a titled manufactured home moves into and out of the state. In those circumstances, the assessed value is prorated using whole months.
- Determine the number of days the real property was legally taxable by adding together the number of days in each taxable month.
Hint: September, April, June, and November have 30 days. All the other months have 31 days except for February. February has 28 days except in a leap year, then it has 29 days.
- Determine the actual value per day by dividing the total actual value of the property by 365, or 366 for leap year. Round to the nearest cent.
- Determine the taxable actual value by multiplying the resulting proportion (dollars per day) by the number of taxable days. Round to the nearest dollar.
- Determine the prorated assessed value by multiplying the prorated taxable actual value by the appropriate assessment ratio. Round according to your county’s policy.
- Verify the calculations.
- It is essential to maintain a system to track records with prorated values so the appropriate changes can be made each January 1. See Chapter 3, Specific Assessment Procedures, for details.
Example:
A parcel of real property was taxable on January 1 and becomes exempt on June 1 of a non-leap year. The total actual valuation is $330,000, with $60,000 allocated to the land and $270,000 allocated to the building. The property will be classified as a charitable doctor’s office (9184/9284); however, the current subclassification codes are 2120/2220. Determine the prorated taxable value of the property.
FIRST: Determine the number of taxable and exempt days. The property is taxable from January 1 through May 31:
January ........... 31
February ......... 28
March ............. 31
April ............... 30
May ................ 31
151 Days
June 1 is not included because that is the day it became exempt.
SECOND: Determine the land and improvement actual value per day.
Land:
$60,000 Actual value ÷ 365 Days = $164.38 Per day (2120)
Improvement:
$270,000 Actual value ÷ 365 Days = $739.73 Per day (2220)
THIRD: Determine the prorated taxable and exempt actual values.
Land:
$164.38 Per day × 151 Taxable days = $24,821 Prorated taxable adj. actual value (2120)
$164.38 Per day × 214 Exempt days = $35,177 + 2 Prorated exempt adj. actual value (9184)
Improvement:
$739.73 Per day × 151 Taxable days = $111,699 Prorated taxable actual value (2220)
$739.73 Per day × 214 Exempt days = $158,302 + 1 Prorated exempt actual value (9284)
NOTE: The rounding adjustment is made to the time-frame with the greatest number of days.
FOURTH: Determine the prorated taxable and exempt assessed values.
Land:
$24,821 Prorated taxable actual value × 0.27 Assessment rate = $ 6,702 Assessed taxable value
$35,179 Prorated exempt actual value × 0.27 Assessment rate = $ 9,498 Assessed exempt value
Improvement:
$111,699 Prorated taxable actual value × 0.27 Assessment rate = $30,159 Assessed taxable value
$158,302 Prorated exempt actual value × 0.27 Assessment rate = $42,741 Assessed exempt value
Round the prorated taxable assessed value to the nearest $1.
FIFTH: There are many ways to verify the calculations. The following is one example:
Land:
$24,821 Taxable actual value (2120)
$35,179 Exempt actual value (9184)
$60,000
Improvement:
$111,699 Taxable actual value (2220)
$158,301 Exempt actual value (9284)
$270,000
A record reflecting four subclass codes for the property should appear on the assessment roll: a taxable land code, a taxable improvement code, an exempt land code and an exempt improvement code.
Destroyed or Demolished Property Proration Rule
The assessed value of a real property improvement that is demolished or destroyed is prorated from January 1 of the current year to the date of destruction. The date the property was destroyed is not counted as a taxable day.
The property owner has the responsibility of reporting the real property as destroyed and the date of the occurrence. A demolition permit may serve as notification of destruction. If the destruction or demolition is not reported, the assessor is not required to prorate the value in accordance with § 39-5-117, C.R.S. If the destruction is well publicized, the assessor may wish to initiate a re-inspection of the property or properties involved in the interest of public relations. Statute does not authorize the proration of value for damaged property.
Property improvements destroyed after assessment date.
Whenever any improvements are destroyed or demolished subsequent to the assessment date in any year, it is the duty of the owner thereof or the owner’s agent to promptly notify the assessor of such destruction or demolition and the date upon which the same occurred. In all such cases, such improvements shall be valued by the assessor at the proportion of its valuation for the full calendar year that the period of time in such year prior to its destruction or demolition bears to the full calendar year. Failure of the owner thereof or of the owner’s agent to so notify the assessor prior to the date taxes are levied shall be considered a waiver, and no proportionate valuation by the assessor shall then be required.
§ 39-5-117, C.R.S.
Reclassifying the land associated with a destroyed improvement:
If the improvement is entirely destroyed the assessor must determine how to classify the underlying land on the following assessment date. Non-residential land should be classified as vacant lots, with abstract codes 0200, 0300, or 0400, according to zoning and permitted uses. However, as provided in § 39-1-102(14.4)(b), C.R.S., if the improvement is residential and destroyed by a “natural cause,” the residential land classification shall remain in place for the year of destruction and the two subsequent property tax years. The residential classification may remain in place for additional subsequent property tax years if the assessor determines there is evidence the owner intends to rebuild or locate a residential improvement on the land.
In 2014, § 39-1-123, C.R.S., was created to provide for a reimbursement of property taxes to a property owner whose real and/or business personal property was destroyed by a natural cause. In 2025, § 39-1-123, C.R.S., was repealed and the state reimbursement for properties that were destroyed by a natural cause was eliminated.
Definitions.
(8.4) "Natural cause" means fire, explosion, flood, tornado, action of the elements, act of war or terror, or similar cause beyond the control of and not cause by the party holding title to the property destroyed.
§ 39-1-102, C.R.S.
As provided in § 39-1-102(14.4)(b), C.R.S., if the improvement is residential and destroyed by a "natural cause," the residential land classification shall remain in place for the year of destruction and the two subsequent property tax years. The residential classification may remain in place for addition subsequent property tax years if the assessor determines there is evidence the owner intends to rebuild or locate a residential improvement on the land.
Additionally, if a residential improvement is destroyed, demolished, or relocated after January 1, 2018, § 39-1-102(14.4)(c)(I), C.R.S., allows the residential land classification to stay in place for the year in which the improvements were destroyed, demolished or relocated and one subsequent property tax year as long as the assessor is able to determine that there is evidence that the owner intends to rebuild or locate a residential improvement on the property. The same proration rules apply to these types of residential improvements that are destroyed, demolished or relocated.
When calculating prorated values for destroyed or demolished real property, the most important thing to remember is to prorate only the improvement value. Separate the land value from the improvement value, prorate the improvement value to the date of destruction, then add the land back to the prorated improvement value to arrive at the total taxable value for the property.
Example: Real Property Destroyed or Demolished
A commercial property has an actual value of $605,860, with $100,000 allocated to land and $505,860 allocated to improvements. The building was completely destroyed by explosion and fire on March 12 of the current year. The owner notified the assessor prior to the date taxes were levied. Determine the prorated value of the property.
Please note, you must include the actual value adjustment in the calculation. It is easiest to make that adjustment to the improvement value in the beginning of the calculations.
First: Determine the number of taxable days; do not count the day of destruction. The property is taxable from January 1 through March 11.
January ...........31
February .........28
March .............11
70 Days
Second: Determine the adjusted actual value per day for the improvement. The land value is not prorated.
$505,860 Improvement actual value ÷ 365 Days = $1,385.92 Per day
Third: Determine the prorated taxable adjusted actual value of the improvement.
$1,385.92 Per day × 70 Taxable days = $97,014 Prorated taxable improvement actual value
Fourth: Determine the prorated taxable assessed value of the improvement.
$97,014 Prorated taxable improvement actual value × 0.27 Assessment rate = $26,193.78
$26,193.78 Rounded to the nearest $1 = $26,194 Improvement assessed value
Fifth: Verify the calculations:
$505,860 Actual value imp. × 0.27 Assessment rate = $136,582 Assessed value
$136,582 Assessed value ÷ 365 Days = $374.20 Assessed value per day
$374.20 Assessed value per day × 70 Taxable days = $26,194 Taxable assessed value
365 Days - 70 Taxable days = 295 Non-Taxable days
$374.20 Per day × 295 Non-taxable day = $110,389 -1 Non-taxable assessed value
$110,388 Non-taxable assessed value + $26,194 Taxable assessed value = $136,582
A record reflecting the full land value and the prorated improvement value should appear on the assessment roll.
Tax Calculation:
Determine the amount of the tax bill the owner will receive in January assuming a tax rate of 0.043270 (43.270 mills.)
Determine the total taxable assessed value of the property by adding the assessed value of the land to the prorated assessed value of the improvements.
$100,000 Actual value land × 0.27 Assessment rate = $27,000 Assessed value land
$26,164 Assessed value impr + $27,000 Assessed value land = $53,164 Total assessed value
Multiply the total assessed value by the tax rate to determine the taxes due.
$53,164 Total assessed value × 0.043270 Tax rate = $2,300 Tax
Property Changing Taxable Status
A change in tax status occurs when a governmental entity buys or sells property, or when the Administrator issues a determination granting exemption, a forfeiture, or a revocation. A change in tax status also occurs when real property is used for governmental purposes and is leased or rented, for at least a one-year term, to the state, a political subdivision, or a state-supported institution of higher education, § 39-3-124(1)(b)(I)(A).
If an exempt property becomes taxable or a taxable property becomes exempt for a portion of the assessment year, general proration rules are used to determine the number of taxable days, the actual value per day, the prorated actual value, and the prorated assessed valuation. As illustrated previously, this is accomplished by determining the number of taxable days, multiplying the number of taxable days by the actual value per day, and then multiplying by the appropriate assessment ratio.
Exemption Proration Rules
First: Determine the number of days the real property was legally taxable by adding together the number of days in each month.
Note: The date the exemption was granted is not taxable. The date the exemption was lost is taxable.
Exemption for governmental entities is determined by the delivery date of the deed; the property is exempt for the number of days the exempt entity held title. Refer to Title Conveyance, Chapter 3, Specific Assessment Procedures, for additional information on deed priority dates.
Priority of deed dates:
- Date of delivery; date title passes to the grantee (shown in the signature area of the deed).
- Acknowledgment date; date deed signed by grantor and acknowledged by a notary public.
- Date made; date deed was prepared.
- Recording date; date deed was recorded by the clerk and recorder.
Second: Divide the actual value of the land and improvement by 365 days (366 for leap year) to find the value per day for each.
Third: Multiply the value per day by the number of taxable days. Multiply the value per day by the number of exempt days.
Fourth: If a determination involves a percentage of the property, a double calculation is required. The number of days the property was 100 percent taxable must be multiplied by the value per day. This total is then added to the total value for the number of days exempt, multiplied by the value per day, and then multiplied by the percent taxable. See Example 2.
Fifth: Sum the taxable value and the exempt values to verify they equal the full actual value. See Example 1.
A record reflecting four subclass codes for the property should appear on the assessment roll; a taxable land code, a taxable improvement code, an exempt land code and an exempt improvement code.
Example 1:
Owner A was granted exemption effective April 15 of the current year. The total property actual value is $99,460, with $24,000 allocated to the land and $75,460 allocated to the building.
First: Determine the number of taxable and exempt days.
January .............31
February ...........28
March ...............31
April .................14
104 Taxable days
April ................ 16
May ................. 31
June ................. 30
July .................. 31
August ............. 31
September ....... 30
October ............ 31
November ........ 30
December ........ 31
261 Exempt days
Second: Determine the land and improvement actual values per day.
Land:
$24,000 Actual value ÷ 365 Days = $65.75 Per day
Improvement: $75,460 Actual value ÷ 365 Days = $206.74 Per day
Third: Determine the taxable actual value and exempt actual value.
Land:
$65.75 Per day × 104 Taxable days = $6,838 Taxable actual value
$65.75 Per day × 261 Exempt days = $17,160.75 ($17,161) Exempt actual value
Improvement:
$206.74 Per day × 104 Taxable days = $21,500.96 ($21,501) Taxable actual value
$206.74 Per day × 261 Exempt days = $53,959.14 ($53,959) Exempt actual value
Fourth: The exemption involves 100 percent of the property; thus, this step is unnecessary.
Fifth: Sum the taxable and exempt values to verify they equal the full actual value.
$ 6,838 Taxable actual value
$17,161 (+1) Taxable actual value
$24,000
$21,501 Taxable actual value
$53,959 Exempt actual value
$75,460
Note: $1 was added to the taxable land value because it is the largest of the land values.
Example 2:
Owner B lost exemption on 64 percent of the real property effective November 11 of the current year. The total property actual value is $230,877 with $55,410 allocated to the land and $175,467 allocated to the building.
Note: The property is 100 percent exempt from January 1 thru November 10 and 64 percent taxable from November 11 to December 31.
First: Determine the number of taxable and exempt days.
January ................. 31
February ............... 28
March ................... 31
April ..................... 30
May ...................... 31
June ...................... 30
July ....................... 31
August .................. 31
September ............ 30
October ................. 31
November ............. 10
314 Exempt days
November ......... 20
December .......... 31
51 Partially taxable days
Second: Determine the land and improvement actual values per day.
Land:
$55,410 Actual value ÷ 365 Days = $151.81 Per day
Improvement:
$175,467 Actual value ÷ 365 Days = $480.73 Per day
Third: Determine the taxable actual value and exempt actual value.
Land:
$151.81 Per day × 51 Partially taxable days = $7,742 Partially taxable actual value
$151.81 Per day × 314 Exempt days = $47,668 Exempt actual value
Improvement:
$480.73 Per day × 51 Partially taxable days = $24,517 Partially taxable actual value
$480.73 Per day × 314 Exempt days = $150,949 Exempt actual value
Fourth: Determine the taxable and exempt value for the partially exempt period of time.
Land:
$7,742 Partially taxable actual value × 64% = $4,955 Taxable actual value for 51 days
$7,742 Partially taxable actual value × 36% = $2,787 Exempt actual value for 51 days
Improvement:
$24,517 Partially taxable actual value × 64% = $15,691 Taxable actual value for 51 days
$24,517 Partially taxable actual value × 36% = $8,826 Exempt actual value for 51 days
Fifth: Sum the taxable and exempt values to verify they equal the full actual value.
Land:
$47,668 Exempt actual value for 314 days
$ 4,955 Taxable actual value for 51 days
$ 2,787 Exempt actual value for 51 days
$55,410
Improvement:
$150,949 (+1) Exempt actual value for 314 days
$ 15,691 Taxable actual value for 51 days
$ 8,826 Exempt actual value for 51 days
$175,467
Note: $1 was added to the exempt improvement value because it is the largest of the improvement values.
Example 3:
Non-residential land and improvements of a previously exempt organization are sold to a non-qualifying organization on August 1. The total actual value of the property is $495,000, with $118,800 allocated to the land and $376,200 allocated to the building. Determine the prorated taxable assessed value.
First: Determine the number of taxable and exempt days.
August 31
September 30
October 31
November 30
December 31
153 Days
Second: Determine the land and improvement actual values per day.
Land:
$118,800 Actual value ÷ 365 Days = $325.48 Per day
Improvement:
$376,200 Actual value ÷ 365 Days = $1,030.68 Per day
Third: Determine the taxable actual value and exempt actual value.
Land:
$325.48 Per day × 153 Taxable days = $49,798 Taxable actual value
$325.48 Per day × 212 Exempt days = $69,002 Taxable actual value
Improvement:
$1,030.68 Per day × 153 Taxable days = $157,694 Taxable actual value
$1,030.68 Per day × 212 Exempt days = $218,504 Exempt actual value
Fourth: The exemption involves 100 percent of the property; thus, this step is unnecessary.
Fifth: Sum the taxable and exempt values to verify they equal the full actual value.
Land:
$ 49,798 Taxable actual value
$ 69,002 Exempt actual value
$118,800
Improvement:
$157,694 Taxable actual value
$218,504 (+2) Exempt actual value
$376,200
Note: $2 was added to the exempt value because it is the largest value.
Rotary Drilling Rig/Portable Equip. Apportionment
Rotary oil and gas drilling rigs, also called rotary rigs, and movable and portable equipment are personal property. They are subject to special apportionment rules. The actual value of a drilling rig, or the movable or portable equipment is divided among the counties where the property was located the previous year.
Owners of movable or portable equipment are required to file a statement accompanying the personal property declaration schedule indicating the counties in which the property is apt to be located during the assessment year, § 39-5-113, C.R.S. The county assessor then apportions the value based on the proposed location(s) during the year and notifies the owner and the other county assessors of the value and apportionment. If an assessor discovers that property was located in his or her county for a period of time that is different from the original apportionment, the county assessor discovering the error must request an amended apportionment. Failure to request an amended apportionment shall permit the original apportionment to stand, § 39-5-113(3), C.R.S.
Each year not later than April 15, rig owners are required to submit a rig location log for each rig they operated during the previous year. They submit the logs to the county of original assessment, that is, the county where the rig was first located during the previous year. This procedure is pursuant to § 39-5-113.3, C.R.S.
Apportionment occurs after the actual value of a rig has been determined by the county of original assessment. The actual value is divided by 365 to determine the actual value per day (366 for leap years). The actual value per day is then multiplied by the number of days the rig was located in each county to determine the apportioned value.
The county of original assessment notifies each Colorado county of its apportionment of the rig’s actual value and sends a copy of the log and apportionment. The company is notified in the same way. Both notifications must occur on or before June 15, § 39-5-113.3, C.R.S. Sections 39-5-121(1.5) and (1.7), C.R.S., requires that notices of value be sent to owners of personal property or upon the taxpayers request, the NOV may be sent electronically; therefore, the county of original assessment is responsible for mailing the Notice of Valuation to the rig owner. The notice should state the total value of the rig. Notices of Valuation may be mailed by the counties receiving an apportioned value, but this is purely optional. If the rig owner wishes to file a protest on the rig value assigned by the assessor, the owner must file a protest with the county of original assessment.
Travel days are assigned to the destination county. Stacked rig days are assigned to the county in which the rig was stacked. Final actual value rounding errors, either plus or minus, are assigned to the county of original assessment.
If assessor errors are found after the original apportionment but before August 1, the county of original assessment may submit a revised apportionment to the owner and other counties involved. Operator errors can only be corrected by the county of original assessment and only prior to August 10. After August 10, no changes can be made due to the August 25 Abstract of Assessment deadline.
Example: Rig Apportionment
The rig operator submits the following log to the county of original assessment. The assessor determines the actual value of the rig to be $750,000. Determine the apportioned actual value that should be assigned to each county.
First: Determine the number of taxable days attributable to each county. Calculate the number of days for each well.
| Well Name | County | Date-From | To | #Days |
|---|---|---|---|---|
| Idler #2 | Prowers, CO | 01-01 | 01-23 | 23 |
| Twombly #1-12 | Cimmaron, OK | 01-24 | 02-09 | 17 |
| Robbins Ranch “A” #1 | Baca, CO | 02-10 | 03-18 | 37 |
| Idler “F” #1 | Prowers, CO | 03-19 | 05-01 | 44 |
| Pinkard #1 | Baca, CO | 05-02 | 06-28 | 58 |
| Hoffman-Federal #1 | Prowers, CO | 06-29 | 07-28 | 30 |
| Buxton #1 | Bent, CO | 07-29 | 08-08 | 11 |
| Hinrich #1 | Wallace, KS | 08-09 | 08-28 | 20 |
| Bailey Farms,Inc. #4 | Prowers, CO | 08-29 | 10-19 | 52 |
| Hudson-Persyn #1 | Bent, CO | 10-20 | 11-02 | 14 |
| Negley “A” #1 | Kiowa, CO | 11-03 | 12-03 | 31 |
| Hefley #2 | Baca, CO | 12-04 | 12-31 | 28 |
| Total | 365 |
Second: Determine the actual value per day.
$750,000 Actual value ÷ 365 Days = $2,054.79 Per day
Third: Determine the apportioned taxable actual value attributable to each county.
| Days × $2,054.79 | Actual Value | |
|---|---|---|
| Days in Baca County, CO | 123 × $2,054.79 | $252,739 |
| Days in Bent County, CO | 25 × $2,054.79 | 51,370 |
| Days in Kiowa County, CO | 31 × $2,054.79 | 63,698 |
| Days in Prowers County, CO | 149 × $2,054.79 | 306,164 + 2 |
| Days in Wallace County, KS | 20 × $2,054.79 | 41,096 |
| Days in Cimmaron County, OK | 17 × $2,054.79 | 34,931 |
| Total | $750,000 |
Note: $2 was added to Prowers County to account for the rounding error because it is the county of original assessment.
Manufactured Homes
Titled manufactured homes are prorated by month when the owner notifies the assessor that the home will be moved out of state or a manufactured home moves into the county from out of state, §§ 39-5-204(1)(c)(II) and 205(3)(b), C.R.S. The value is not prorated if a titled manufactured home is moved to another county in the state or when the home is moved within the county. Upon notification to the treasurer, the taxes become due and payable for the full calendar year to the county in which it was located on January 1, if the home is removed from the county, § 39-5-205(3)(a), C.R.S.
A fraction of any month is counted as a full month if the titled manufactured home leaves the state on or after the 16th. The assessed value of the titled manufactured home is divided by 12 to determine the assessed value per month. The assessed value per month is then multiplied by the number of taxable months to arrive at a prorated assessed value. The prorated assessed value is then multiplied by the tax rate (previous year if tax rate has not been set) to determine taxes dues.
Example: Manufactured Home Out-of-State Move
A titled manufactured home, which was in the county on the assessment date, has an assessed value of $5,020. The home is permitted to move out of state on May 15. The tax rate is 0.103680. Determine the prorated tax.
First: Determine the number of taxable months. The home is taxable from January through April. May is not counted because the home was not in the county on or after the 16th.
January + February + March + April = 4 Months
Second: Determine the taxable assessed value per month. Round to the nearest cent.
$5,020 Total assessed value ÷ 12 Months = $418.33 Per month
Third: Determine the prorated taxable assessed value. Round to the nearest dollar.
$418.33 Per month × 4 Months = $1,673 Taxable assessed value
Fourth: Multiply the prorated taxable assessed value by the tax rate to determine the taxes due prior to movement of the titled manufactured home.
$1,670 Taxable assessed value × 0.103680 Tax rate = $173.15 Tax
Example: Titled Manufactured Home In-State Move
A titled manufactured home was delivered to Cheerful Manufactured Home Park in Shine County, Colorado on May 17 from Nebraska. The titled manufactured home has an assessed value of $3,264. The tax rate is 0.081432. Determine the prorated tax.
First: Determine the number of taxable months. The home is taxable from June through December. May is not counted because the home was not in the county prior to the 16th.
June + July + August + September + October + November + December = 7 Months
Second: Determine the taxable assessed value per month. Round to the nearest cent.
$3,264 Total assessed value ÷ 12 Months = $272.00 Per month
Third: Determine the prorated taxable assessed value. Round to the nearest dollar.
$272.00 Per month × 7 Months = $1,904 Taxable assessed value
Fourth: Multiply the prorated taxable assessed value by the tax rate to determine the taxes due prior to movement of the titled manufactured home.
$1,904 Taxable assessed value × 0.081432 Tax rate = $155.05 Tax
Titled manufactured homes which are located on sales display lots of manufactured home dealers and listed as inventories of merchandise by the dealer are exempt, § 39-5-203(3)(a), C.R.S. If the manufactured home becomes part of the dealer’s inventory and located on a display lot, the value is prorated by the day, based on the date the home changed taxable status.
New or used manufactured homes taken in trade or purchased by dealers and which remain on locations other than the dealer’s sales display lot are taxable.
Note: If the manufactured home remains in dealer inventory, the dealer is not required to obtain a new Certificate of Title, § 38-29-115, C.R.S.
Example: Manufactured home traded in on new manufactured home
A used titled manufactured home is traded in on a new titled manufactured home. The ownership of the used home is transferred to the dealer, moved to the dealer’s sales display lot, and listed as inventory August 1. The ownership change of the new titled manufactured home is also effective August 1. The actual value of the used home is $10,500. The new home as an actual value of $157,500. Calculate the prorated taxable value for each home.
First: Determine the number of taxable and exempt days.
The used home is taxable from January 1 through July 31:
January 31
February 28
March 31
April 30
May 31
June 30
July 31
212 Days
The new home is taxable from August 1 through December:
August 31
September 30
October 31
November 30
December 31
153 Days
Second: Determine the used and new home actual value per day.
Used home:
$10,500 Actual value ÷ 365 Days = $28.77 Per day (1235)
New home:
$157,500 ÷ 365 Days = $431.51 Per day (1235)
Third: Determine the prorated taxable and exempt actual values.
Used home:
$28.77 Per day × 212 Taxable days = $6,099 – $1 Prorated taxable actual value (1235)
$28.77 Per day × 153 Exempt days = $4,402 Prorated exempt actual value (1235)
New home:
$431.51 Per day × 153 Taxable days = $66,021 Prorated taxable actual value (1235)
$431.51 Per day × 212 Exempt days = $91,480-1 + 1 Prorated exempt actual value (1235)
Note: The rounding adjustment is made to the time-frame with the greatest number of days.
Fourth: Determine the prorated taxable and exempt assessed values.
Used home (Schools):
$6,098 Prorated taxable actual value × .0705 Assessment rate = $430 Assessed taxable value
$4,402 Prorated exempt actual value × .0705 Assessment rate = $310 Assessed exempt value
Used home (Local Government):
$6,098 Prorated taxable actual value × .0625 Assessment rate = $381 Assessed taxable value
$4,402 Prorated taxable actual value × .0625 Assessment rate = $275 Assessed taxable value
New home (Schools):
$66,021 Prorated taxable actual value × .0625 Assessment rate = $4,126 Assessed taxable value
$91,479 Prorated exempt actual value × .0625 Assessment rate = $5,717 Assessed exempt value
Round the prorated taxable assessed value to the nearest $1.
Fifth: There are many ways to verify the calculations. The following is one example:
Used home:
$ 6,098 Taxable actual value (1235)
$ 4,402 Exempt actual value (1235)
$10,500 Actual value
New home:
$ 66,021 Taxable actual value (1235)
$ 91,479 Exempt actual value (1235)
$157,500 Actual value